微搜索再放异彩：多目标组合优化问题求解-凯发k8官网下载客户端

孟子曰：“鱼，我所欲也；熊掌，亦我所欲也。二者不可得兼，舍鱼而取熊掌者也。”在实际生产生活中，人们往往更希望鱼与熊掌兼得。例如，人们希望在降低服装购买成本的情况下使其舒适度最大化，或者希望在减少车辆能耗和污染物排放的情况下使车辆性能最优化。

图1 生活中的多目标组合优化问题

一、错综复杂：多目标组合优化问题

多目标组合优化问题（multiobjective combinatorial optimization problem, mocop）是涉及多个目标函数同时优化的数学问题[2]，需要权衡两个或多个相互冲突的目标，进而做出最优决策。目前，该问题已被应用于工程、经济、物流等多个领域。mocop的基本数学模型如公式(1)所示。

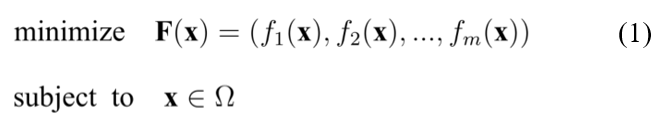
当多目标组合优化问题的解在目标空间分布的距离与决策空间分布的距离呈非正相关关系时，现有算力分配方法的求解性能会变差[3-6]。这将导致相邻目标向量所对应的决策向量差异性大。例如，图2中y1和y2是两个相邻的目标向量，x1和x2是决策空间中对应的两个解。如果x1和x2所属的决策空间不相邻，那么从一个子问题的解转移到其相邻子问题的解是十分困难的。这导致现有的基于分解算法的算力分配方法在求解mocops时的性能会变差。

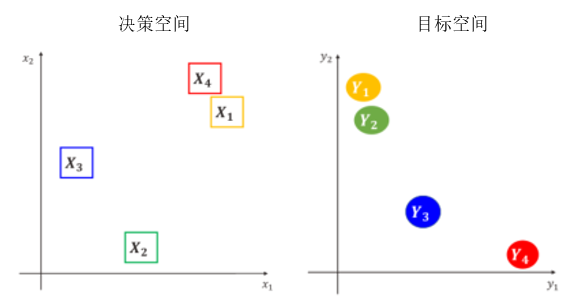
图2 目标空间的距离与决策空间的距离非正相关示例

如何选择子问题并合理分配有限的算力是提升基于分解算法求解mocops性能的关键之一。因此，针对背包与二次分配多目标组合优化问题存在的相邻目标向量所对应的决策向量差异程度大这一问题，智能算法研究中心的研究人员提出基于稀疏目标子区域微搜索的多目标组合优化算法（local-diversity evaluation assignment strategy for decomposition-based multiobjective evolutionary algorithm, moea/d-ldea）[1]。moea/d-ldea通过划分目标空间获得微小的多目标子区域，使算法能够在多目标组合优化问题的大规模搜索空间中找到有效决策子集，并依据多目标子区域的稀疏度动态分配算力，在不同的子区域进行定向搜索，节省了计算代价，最终获得多目标组合优化问题的高质量解集。目前，该研究工作已发表在国际顶级期刊ieee transactions on systems, man, and cybernetics: systems（jcr一区，影响因子11.471）。

moea/d-ldea算法的流程如图3所示。该算法主要包括两部分：微小搜索子区域的稀疏度评估模型和有效决策子集的算力分配策略ldea。

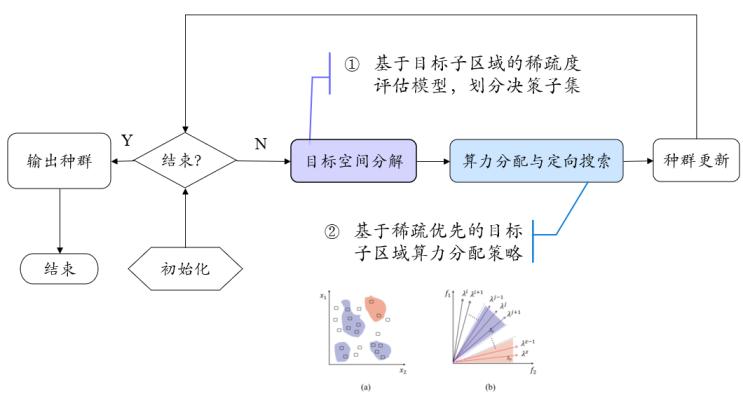
图3 moea/d-ldea算法流程图

二、排沙简金：微小搜索子区域的稀疏度评估模型

微小搜索子区域是通过在多目标优化问题中使用分解算法来确定的。分解算法将多目标问题分解为一组单目标子问题，每个子问题都是在不同权重向量下的优化目标函数。因此，搜索空间的规模仅限于每个单目标问题的权重向量，而不是整个多目标问题的搜索空间。算法将在微小范围内进行定向搜索，这样极大地减少了计算成本，节省了算力。

微小搜索子区域的稀疏度评估模型主要用于估计每个目标子区域的局部密度。首先，假定目标空间被划分为k个目标子区域，其中，可以被定义为：

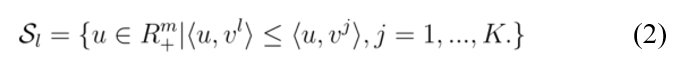
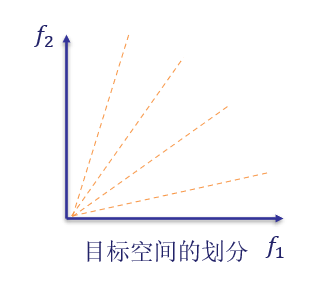
图4 微小搜索子区域的稀疏度评估模型对目标空间的划分

当目标空间被划分为多个子区域后，由于每个解与一个目标子区域相关联，因此可以通过采用公式(3)计算与目标子区域相连的解的个数来估计目标子区域的局部密度：

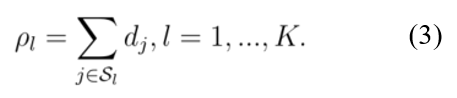
其中， 表示在种群c中由得到适应值评估的第j个子问题所生成的解的数量，其中c包含e(e ≤ n)个在各个目标均不相等时适应度值的解。

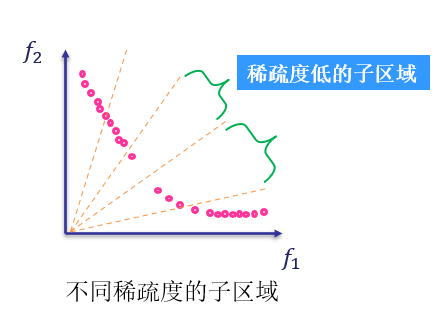
图5 目标空间中不同稀疏度的子区域

如公式(4)所示，当局部密度值与所选目标子区域的概率成反比，即目标子区域稀疏度越高，则目标子区域被选择的概率越大。被选中的目标子区域即为该微搜索过程的有效决策子集。

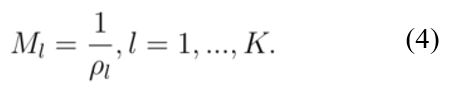
最后，可以根据目标子区域的稀疏度，采用公式(5)计算被选定目标子区域的概率，即：

1. 称体载衣：有效决策子集的算力分配策略

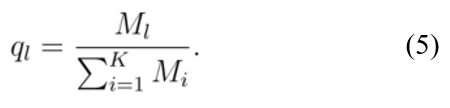
因为搜索算法倾向于更频繁地探索多样性更强的区域，所以搜索算法的效率取决于搜索空间不同部分之间的差异程度。因此，我们提出有效决策子集的算力分配策略ldea，将算力分配给具有较低目标函数值和较高多样性的个体，实现算力的相对均匀分配，从而减少不必要的算力消耗，节省计算成本。

当mocops的解满足目标空间距离与决策空间距离呈非正相关的前提时，在有效决策子集中确定权重向量的子问题z（如图6(b)所示），可以使有效决策子集中的子问题z比其它子问题获得更多的适应度评估次数。ldea策略对不同有效决策子集所关联的不同子问题进行不均等的算力分配，避免算力冗余或者被重复分配，最终在确定被选中的子问题后生成解。

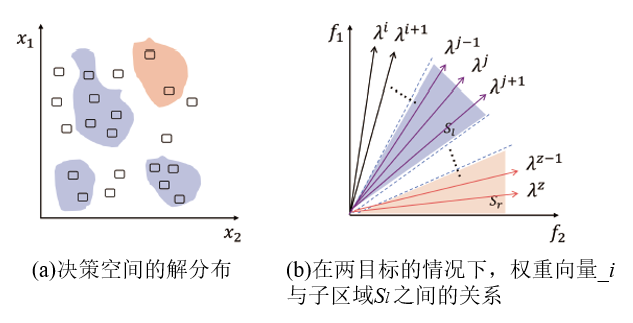
图6 采用ldea策略对子问题进行选择的过程说明

为了验证ldea策略的有效性，研究人员评估了moea/d-ldea与四个对比算法在momkp 实例和mqap实例上所获得的反向世代距离（inverted generational distance, igd）和超体积（hypervolume, hv）指标值。

表1 moea/d-ldea 与对比算法在求解momkp测试问题上所获得的igd和hv指标值

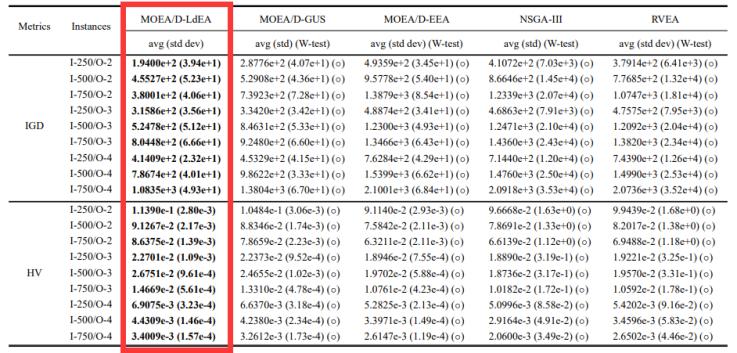
表2 moea/d-ldea 与对比算法在求解mqap测试问题上所获得的igd和hv指标值

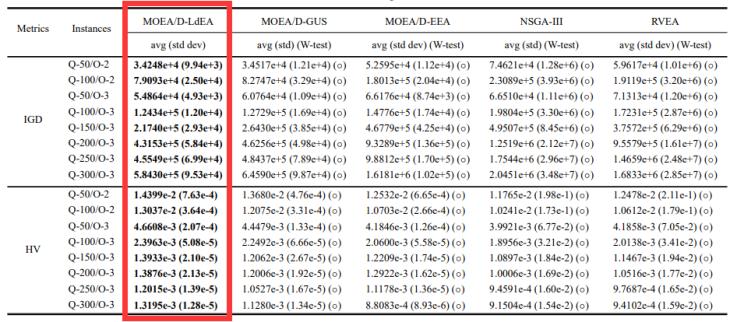
从表1和表2可见，moea/d-gus在移除了ldea策略后对momkp实例和 mqap实例进行求解所得的igd值和hv值差于moea/d-ldea所获得的igd值和hv值。这验证了采用ldea策略求解满足目标空间距离与决策空间距离非正相关的空间化目标先验特性的momkp和mqap测试问题的有效性。此外，moea/d-ldea能够在多个有效决策子集中实现分配更少的算力来获得高质量的非支配解，具备较好的折衷收敛性与多样性，从而在所获得的igd值和hv值上优于moea/d-eea、nsga-iii和rvea。

图7展示了moea/d-ldea与四个对比算法在 momkp 测试问题和mqap测试问题上获得的最终解集。与采用不同算力分配策略的其他对比算法相比，moea/d-ldea获得的解集更逼近帕累托前沿（praeto front, pf）。这说明通过确定微小搜索子区域和有效决策子集算力分配策略，moea/d-ldea可以在目标空间的更多有效决策子集获得更优的最终解集，克服从一个子问题的解转移到其邻近子问题的解这一困难，更有利于解决 mocops。

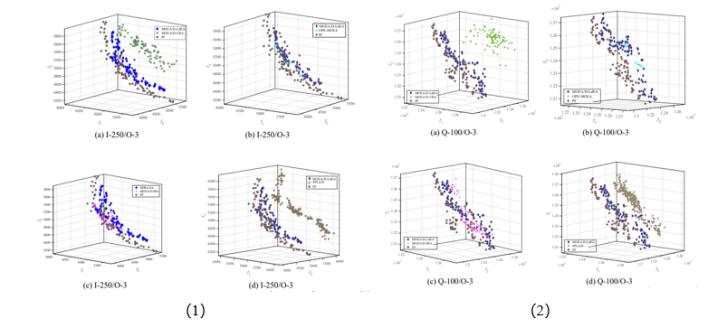
图7 moea/d-ldea、moea/d-cra、ope-moea、moea/d-ira 和ppls/d 在momkp (1) 和mqap (2) 实例上获得的最终解集

综上所述，moea/d-ldea通过运用微搜索方法选定目标子区域，然后将选中的目标子区域作为定向搜索方向并分配更多的算力，在求解背包问题、二次分配问题等多目标组合优化问题方面获得了显著成效，在性能上明显优于ope-moea、ppls/d等现有算力分配的算法。

长期以来，智能算法研究中心致力于运用微搜索算法解决我国实际工业生产中的“卡脖子”难题，目前已在柔性车间生产调度[10]和滤波器调参[11]问题上初见成效。今后，我们将尝试使用代理模型与微搜索算法相结合的方法求解超大规模的复杂组合优化问题，从而提升微搜索算法的求解速度，以适应当今发展迅速的工业时代。

参考文献

1. s. yang, h. huang, f. luo, y. xu and z. hao, “local-diversity evaluation assignment strategy for decomposition-based multiobjective evolutionary algorithm,” ieee transactions on systems, man, and cybernetics: systems, vol. 53, no. 3, pp. 1697-1709, 2023.
2. k. miettinen, nonlinear multiobjective optimization. new york, ny, usa: springer, 1998.
3. q. zhang, w. liu and h. li, “the performance of a new version of moea/d on cec09 unconstrained mop test instances,” in ieee congress on evolutionary computation (cec), 2009, pp. 203-208.
4. a. zhou and q. zhang, “are all the subproblems equally important? resource allocation in decomposition-based multiobjective evolutionary algorithms,” ieee transactions on evolutionary computation, vol. 20, no. 1, pp. 52-64, 2016.
5. q. lin, g. jin, y. ma, k.c. wong, c. a. c. coello, j. li, j. chen and j. zhang, “a diversity-enhanced resource allocation strategy for decomposition-based multiobjective evolutionary algorithm,” ieee transactions on cybernetics, vol. 48, no. 8, pp. 2388-2401, 2018.
6. s. yao, z. dong, x. wang and l. ren, “a multiobjective multifactorial optimization algorithm based on decomposition and dynamic resource allocation strategy,” information sciences, vol. 511, pp. 18-35, 2020.
7. q. kang, x. song, m. zhou and l. li, “a collaborative resource allocation strategy for decomposition-based multiobjective evolutionary algorithms,” ieee transactions on systems, man, and cybernetics: systems, vol. 49, no. 12, pp. 2416-2423, 2019.
8. h. chen, g. wu, w. pedrycz, p. n. suganthan, l. xing and x. zhu, “an adaptive resource allocation strategy for objective space partition-based multiobjective optimization,” ieee transactions on systems, man, and cybernetics: systems, vol. 51, no. 3, pp. 1507-1522, 2021.
9. j. shi, q. zhang and j. sun, “ppls/d: parallel pareto local search based on decomposition,” ieee transactions on cybernetics, vol. 50, no. 3, pp. 1060-1071, 2020.
10. j. su, h. huang, g. li, x. li and z. hao, “self-organizing neural scheduler for the flexible job shop problem with periodic maintenance and mandatory outsourcing constraints, ” ieee transactions on cybernetics, doi: 10.1109/tcyb.2022.3158334.
11. h. huang, f. feng, s. huang, l. chen and z. hao, “micro-scale searching algorithm for coupling matrix optimization of automated microwave filter tuning,” ieee transactions on cybernetics, doi: 10.1109/tcyb.2022.3166225.